If you’ve ever solved equations, worked with data, or coded in Python, you’ve already met matrices—even if you didn’t realize it.
Let’s break down what a matrix actually is, why it matters, and how it connects to the rest of mathematics.
What Is a Matrix in Simple Terms?
A matrix is a rectangular grid of numbers arranged in rows and columns.
Each position in that grid holds a value, called an element.
For example:
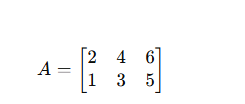
Matrix A has 2 rows and 3 columns — we call this a 2×3 matrix (read “two by three”).
Every value inside it can be labeled by its row and column position, such as (a_{12}) for “row 1, column 2.”
This structure makes matrices incredibly useful for organizing and computing sets of related numbers — from equations to images.
The Formal Definition
In mathematics, a matrix is denoted as:
A=[ aij ] m×n
- (a_{ij}) → element at the i-th row and j-th column
- (m) → number of rows
- (n) → number of columns
When (m = n), the matrix is square. Square matrices are the foundation for operations like finding a determinant or computing an inverse matrix.
If you’d like to experiment with this, you can try the Inverse Matrix Calculator — it instantly finds the inverse of any square matrix.
Types of Matrices
Different shapes and values give matrices special names and properties.
Here are the most common ones you’ll encounter:

👉 You can explore each structure further in our guide on Types of Matrices.
Matrix Operations You Should Know
Matrices can be combined and transformed using algebraic rules.
Here are the essential operations:
1. Addition and Subtraction
Possible only when both matrices have the same dimensions.
C=A+B=[ aij+bij ]
2. Scalar Multiplication
Multiply every element by a constant value (called a scalar).
3. Matrix Multiplication
Rows of the first matrix interact with columns of the second.
Used in transformations, graphics, and data modeling.
4. Determinant
A single number representing certain properties of a square matrix — used to check if it’s invertible.
You can calculate it instantly with the Determinant Calculator.
5. Inverse of a Matrix
The “reciprocal” of a matrix. If (A^{-1}) exists,
A×A−1=I
where (I) is the identity matrix.
Try the 3×3 Matrix Inverse Calculator to see this in action.
Matrix Notation and Symbols
Matrices are labeled with capital letters (A, B, C).
Their elements use lowercase letters with subscripts (a₁₁, a₁₂, etc.).
The transpose, written as (A^T), flips rows into columns.
Transpose operations are essential in the Gauss–Jordan method and linear transformations.
How Matrices Represent Linear Equations
A system of linear equations can be rewritten compactly using a matrix:
AX=B
Where:
- (A) = coefficients
- (X) = variables
- (B) = constants
This notation simplifies solving multiple equations at once.
If (A) is invertible, the solution is (X = A^{-1}B).
You can experiment with this setup in our System of Equations Calculator.
Real-World Uses of Matrices
Matrices go far beyond classroom math. They power most of the technology you use daily.
Computer Graphics:
3D games and design software rely on transformation matrices to rotate, scale, and move objects in space.
Machine Learning:
Every dataset and neural network layer is built on matrices — storing inputs, weights, and outputs.
Data Science:
Matrices organize datasets for regression, clustering, and dimensionality reduction.
Engineering and Physics:
Used in structural analysis, circuit design, and control systems.
Cryptography:
Matrix multiplication helps encode and decode information for secure communication.
Why Understanding Matrices Matters
Learning about matrices isn’t just about passing linear algebra — it’s about understanding the language of data and structure.
They help you model relationships, visualize geometry, and solve problems that scale with technology.
Once you understand the foundation, you can explore advanced topics like:
- How to Calculate the Inverse of a Matrix
- Matrix Inversion Explained
- Matrix Inverse in Machine Learning
Each builds on the core idea of what a matrix is — an organized, logical way to describe relationships between numbers.
Quick Summary
| Concept | Description |
|---|---|
| Matrix | Rectangular grid of numbers or expressions |
| Elements | Individual entries in the grid |
| Order (m×n) | Rows × Columns |
| Square Matrix | Equal rows and columns |
| Key Uses | Data representation, graphics, ML, cryptography |
Frequently Asked Questions
What is a matrix in mathematics?
It’s an array of numbers arranged in rows and columns that helps represent linear equations, data, and transformations.
What is the order of a matrix?
The size of a matrix, expressed as rows × columns (for example, 3×2).
Why do we use matrices?
Matrices make it easy to model and compute systems that involve multiple variables simultaneously.
Can every matrix be inverted?
Only square matrices with a non-zero determinant have an inverse.
