Once you know what a matrix is, the next step is learning how to work with matrices.
Matrix operations form the foundation of linear algebra — they’re how we combine, transform, and solve systems of equations efficiently.
In this guide, we’ll go step-by-step through each major matrix operation, show how it works, and explain when to use it.
What Are Matrix Operations?
Matrix operations are the set of mathematical actions that can be performed on matrices — much like addition or multiplication with regular numbers.
They allow you to:
- Add or subtract data tables
- Scale entire matrices by a constant
- Multiply matrices to represent transformations
- Compute the determinant or inverse for solving equations
If you’re new to matrices, start with our guide on What Is a Matrix before diving into these operations.
1. Matrix Addition
You can add two matrices if they have the same dimensions (same number of rows and columns).
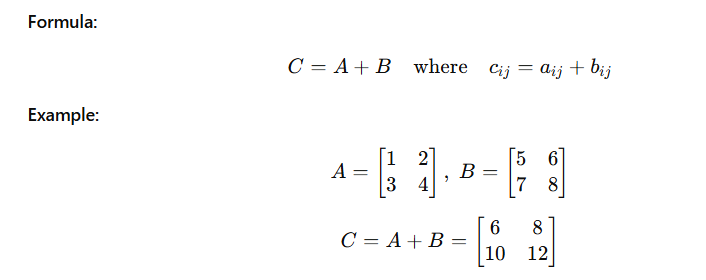
Matrix addition is often used to combine data sets or accumulate results in algorithms.
2. Matrix Subtraction
Just like addition, subtraction works element-by-element for matrices of the same order.
Formula:
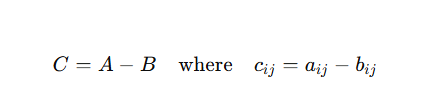
It’s commonly used in error analysis or comparing transformations.
3. Scalar Multiplication
You can multiply a matrix by a scalar (a single number) to scale every element.

This operation is used for adjusting weights, brightness, or other proportional quantities in real data.
4. Matrix Multiplication
Matrix multiplication is one of the most important operations — it’s how we combine transformations or solve systems of equations.
Rule:
Am×n by Bn×p
The resulting matrix (C) will have dimensions (m \times p).

To experiment with this interactively, try our Matrix Calculators Hub — you can calculate inverses, determinants, and more.
5. Transpose of a Matrix
The transpose flips a matrix over its diagonal — rows become columns and vice versa.
Notation: (AT)
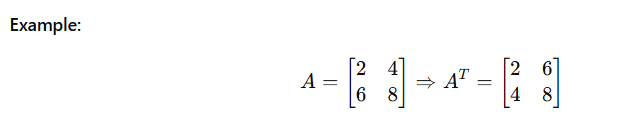
The transpose is essential for symmetry checks, orthogonal matrices, and dot products.
You’ll use this operation often in topics like the Gauss–Jordan Method.
6. Determinant of a Matrix
The determinant is a single number that tells you if a square matrix is invertible and what kind of transformation it represents.
Notation: det ( 𝐴 ) or (A)
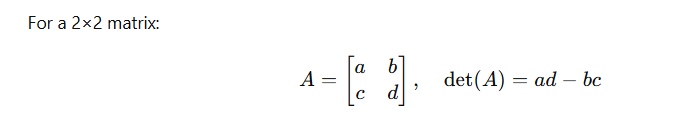
If (\det(A) = 0), the matrix is singular — it has no inverse.
If (\det(A) \neq 0), the matrix is non-singular and can be inverted.
Try it with the Determinant Calculator.
7. Inverse of a Matrix
The inverse of a square matrix (A) is a matrix (A^{-1}) such that:
A×A−1=I
where (I) is the identity matrix.
You can compute it using:
- Adjugate and determinant method
- Gauss–Jordan elimination
- LU decomposition
Finding the inverse is essential in solving systems of equations:
AX=B⇒X=A−1B
You can calculate it instantly with our Inverse Matrix Calculator.
8. Division of Matrices (Conceptual)
There’s no true “division” for matrices, but we can mimic it using the inverse:
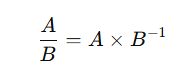
This is used in linear systems and regression models.
If (B^{-1}) doesn’t exist, use the pseudoinverse, explained in our Pseudo Inverse Guide.
9. Trace of a Matrix
The trace is the sum of the diagonal elements of a square matrix.
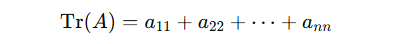
It’s widely used in eigenvalue theory and machine learning to describe transformations.
10. Rank of a Matrix
The rank tells you how many independent rows or columns a matrix has.
It helps identify redundancy in data and detect singular matrices.
High rank = more information.
Low rank = dependencies or linear relationships.
Real-World Examples of Matrix Operations
Matrix operations aren’t just abstract math — they run most of modern computing.
| Field | Example Use |
|---|---|
| Computer Graphics | Matrix multiplication transforms 3D models |
| Machine Learning | Multiplying weight and input matrices |
| Data Science | Covariance and correlation matrices |
| Engineering | Solving equations in electrical or mechanical systems |
| Cryptography | Using modular arithmetic and inverses to encode messages |
For instance, in a 3D video game, each movement or rotation of an object is represented by a transformation matrix multiplied by position vectors in real time.
Summary Table of Matrix Operations
| Operation | Symbol | Description | Example Use |
|---|---|---|---|
| Addition | (A + B) | Combine matrices | Data combination |
| Subtraction | (A – B) | Find difference | Error correction |
| Scalar Multiplication | (kA) | Scale a matrix | Adjusting weights |
| Multiplication | (A \times B) | Combine transformations | 3D rotations |
| Transpose | (A^T) | Flip rows & columns | Symmetry, dot products |
| Determinant | ( | A | ) |
| Inverse | (A^{-1}) | Reverse transformation | Equation solving |
| Trace | (\text{Tr}(A)) | Sum of diagonal | Eigenvalues |
| Rank | rank(A) | Independent rows/cols | Data dimension |
Common Mistakes to Avoid
- Trying to add or multiply matrices with mismatched dimensions
- Forgetting that matrix multiplication is not commutative
((A \times B \neq B \times A)) - Assuming every matrix has an inverse — check the determinant first
- Mixing up row and column order when taking transposes
If you ever get stuck, the Matrix Inversion Guide explains these rules step-by-step.
Frequently Asked Questions
What are the main operations on matrices?
Addition, subtraction, scalar multiplication, matrix multiplication, determinant, inverse, transpose, and rank.
Which matrix operations require the same size?
Addition and subtraction. Multiplication only requires column-row alignment.
Why is matrix multiplication not commutative?
Because the order of combining transformations matters — it changes the result.
What operation gives the identity matrix?
Multiplying a matrix by its inverse: (A \times A^{-1} = I).
