When you first learn matrix inversion, it seems straightforward — until you meet the pseudoinverse.
Both concepts are used to “reverse” a matrix operation, but they’re not the same thing.
This guide explains the difference between the inverse and pseudoinverse, when to use each, and how they connect to real-world problems like solving equations and building AI models.
The Quick Difference
| Feature | Matrix Inverse ((A^{-1})) | Pseudoinverse ((A^+)) |
|---|---|---|
| Matrix Type | Only for square matrices | Works for any rectangular or square matrix |
| Existence | Exists if (\det(A) ≠ 0) | Always exists (for any matrix) |
| Formula | (A⁻¹ = (1 / det(A)) adj(A)) | (A⁺ = (AᵀA)⁻¹ Aᵀ) (for full-rank A) |
| Use Case | Solving exact equations | Solving approximate or overdetermined equations |
| Result Meaning | Exact inverse | Best least-squares approximation |
| Requires | Square, non-singular matrix | Any matrix with or without inverse |
What Is a Matrix Inverse?
The inverse of a matrix (A⁻¹) reverses the effect of (A).
It satisfies: AA⁻¹ = A⁻¹A = I
where (I) is the identity matrix.
The inverse exists only if:
- (A) is square (same number of rows and columns), and
- (det(A)=0).
Example:
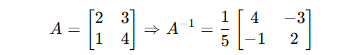
You can compute it instantly using the Inverse Matrix Calculator.
Learn more: Inverse of a Matrix – Formula and Steps
What Is a Pseudoinverse (Moore–Penrose Inverse)?
The pseudoinverse, denoted (A^+), generalizes the idea of an inverse for non-square or singular matrices — cases where a regular inverse doesn’t exist.
It’s formally defined as the Moore–Penrose inverse and satisfies four special conditions (Penrose equations):
- (A A⁺ A = A)
- (A⁺ A A⁺ = A⁺)
- ((A A⁺)ᵀ = A A⁺)
- ((A⁺ A)ᵀ = A⁺ A)
For a full-rank matrix, the pseudoinverse is computed as: A⁺ = (AᵀA)⁻¹ Aᵀ
If (A) is tall (more rows than columns), this gives the least-squares solution.
👉 Use the Pseudo Inverse Calculator to see how it works with real data.
When to Use Each
| Scenario | Correct Choice | Why |
|---|---|---|
| Square and invertible matrix | Regular inverse | Exact reversal possible |
| Rectangular matrix | Pseudoinverse | Regular inverse undefined |
| Singular or rank-deficient matrix | Pseudoinverse | Handles dependent rows or columns |
| Overdetermined systems (more equations than unknowns) | Pseudoinverse | Finds least-squares fit |
| Under-determined systems (more unknowns than equations) | Pseudoinverse | Finds minimal-norm solution |
| Machine learning / regression | Pseudoinverse | Used in closed-form linear regression |
You can check your formula-based solution using our 2×2 matrix inverse calculator in seconds.
Geometric Meaning
- Inverse: Perfectly “undoes” the transformation — maps every output back to its unique input.
- Pseudoinverse: Projects data onto the closest possible solution when no perfect inverse exists.
Imagine rotating and scaling a shape (invertible transformation).
If that shape gets flattened into a line (singular case), you can’t “undo” it — but the pseudoinverse finds the closest 3D approximation of its original form. The cofactor method is easier to verify with the 3×3 matrix inverse calculator after you compute each minor.
Example: Solving a System with Pseudoinverse
Suppose you have an overdetermined system:
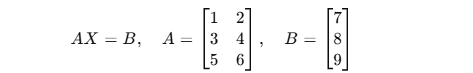
This matrix (A) is 3×2, so it has no true inverse.
We can find (X) using the pseudoinverse: X = A⁺B = (AᵀA)⁻¹ AᵀB
This gives the least-squares solution, minimizing (|AX – B|).
You can perform this operation interactively in our System of Equations Calculator.
Mathematical Relationships
- If (A) is invertible,
then the pseudoinverse equals the regular inverse: A⁺ = A⁻¹ - For rank-deficient matrices: (A⁺) still exists and acts as a generalized inverse.
- (A⁺ A) and (A A⁺) act as projection matrices — projecting onto column or row spaces of (A).
Computational Methods
| Method | Works For | Notes |
|---|---|---|
| Adjugate / Determinant Formula | Small, square matrices | Exact but manual |
| Gauss–Jordan Elimination | Square matrices | Used in most calculators |
| SVD (Singular Value Decomposition) | Any matrix | Stable, accurate for pseudoinverse |
| Normal Equation ((AᵀA)⁻¹ Aᵀ) | Full-rank rectangular matrices | Common in machine learning |
SVD is preferred in data science and numerical computation because it handles rounding errors better than direct inversion. Larger matrices become easier when you use the 4×4 matrix inverse calculator for verification.
Real-World Applications
| Field | Inverse | Pseudoinverse |
|---|---|---|
| Linear Algebra | Solving exact systems | Approximate solutions |
| Machine Learning | Covariance inverses | Linear regression, PCA |
| Computer Graphics | Transformations | Reconstructing 3D poses |
| Engineering | Control systems | Least-squares control design |
| Data Science | Regular matrices | Overdetermined models and fitting |
For example, the normal equation in regression: θ = (XᵀX)⁻¹ Xᵀ y is exactly a pseudoinverse computation. Complex operations become manageable when the 5×5 matrix inverse calculator handles the computation for you.
Example Comparison
| Case | Matrix | Result |
|---|---|---|
| Square invertible | ( 2 & 1 \ 0 & 3 ) | Use regular inverse |
| Rectangular (3×2) | ( 1 & 2 \ 3 & 4 \ 5 & 6\ ) | Use pseudoinverse |
| Singular | ( 2 & 4 \ 1 & 2 \ ) | Use pseudoinverse (inverse undefined) |
Key Differences at a Glance
| Concept | Inverse | Pseudoinverse |
|---|---|---|
| Requires determinant ≠ 0 | ✅ Yes | ❌ No |
| Works on non-square matrices | ❌ No | ✅ Yes |
| Returns exact inverse | ✅ Yes | ❌ Approximate |
| Handles singular matrices | ❌ No | ✅ Yes |
| Used in regression / ML | ❌ Rarely | ✅ Often |
| Computational method | Adjugate / Gauss–Jordan | SVD / Normal equations |
Advantages of the Pseudoinverse
- Works for any matrix shape
- Produces stable results for noisy data
- Gives best-fit solutions when no perfect inverse exists
- Handles overdetermined and underdetermined systems
- Crucial in algorithms like least squares, PCA, and ridge regression
Learn more about its implementation in our Pseudo Inverse Calculator.
Common Misconceptions
- “The pseudoinverse is the same as the inverse.”
→ Only true if the matrix is square and full rank. - “Pseudoinverse is approximate, so it’s inaccurate.”
→ It’s mathematically precise — it gives the best possible solution under given conditions. - “You can always find the inverse.”
→ Not true. Many matrices are singular; that’s when you need (A⁺).
When the matrix is singular, the pseudoinverse calculator provides the proper Moore–Penrose solution.
Frequently Asked Questions
1. Is the pseudoinverse the same as the inverse?
No. The pseudoinverse extends the idea of an inverse to matrices that are not square or not invertible.
2. When should I use the pseudoinverse?
When dealing with rectangular, singular, or large data matrices — especially in regression or optimization.
3. Can a pseudoinverse replace the inverse?
For full-rank square matrices, yes — it gives the same result.
4. How do I compute the pseudoinverse manually?
Use (A⁺ = (AᵀA)⁻¹ Aᵀ) for tall matrices, or software like MATLAB or our Pseudo Inverse Tool.
Summary
| Aspect | Matrix Inverse | Pseudoinverse |
|---|---|---|
| Definition | Exact reverse of a square, non-singular matrix | Generalized inverse valid for any matrix |
| Formula | (A⁻¹ = 1/det(A) · adj(A)) | (A⁺ = (AᵀA)⁻¹ Aᵀ) |
| Applicability | Square matrices only | Square or rectangular |
| Main Use | Exact solution | Least-squares or minimal-norm solution |
Final Takeaway
Both inverse and pseudoinverse help you “undo” matrix operations — but they serve different realities.
The inverse handles perfect, square, full-rank systems.
The pseudoinverse handles the messy, overdetermined, or incomplete ones — the kind that appear in real data and machine learning.
For quick and accurate calculations, explore:
