In the world of mathematics, matrix operations can seem intimidating, but they hold the key to solving complex real-world problems. Among these operations, matrix inversion is one of the most powerful and versatile tools. It plays an essential role in fields like engineering, data science, cryptography, and even business analytics. Understanding how to invert matrices and use an Inverse Matrix Calculator can significantly speed up your problem-solving process and improve your results.
Whether you’re a student, a professional in machine learning, an engineer designing complex systems, or a financial analyst, knowing how to work with inverse matrices will streamline your workflow. This guide is designed to help you understand matrix inversion from the ground up, showing you how it’s used in real-life scenarios and how to easily compute the inverse of matrices using an online calculator.
What is Matrix Inversion?
Matrix inversion is a mathematical operation that takes a square matrix and transforms it into its inverse matrix. The inverse of a matrix, when multiplied by the original matrix, results in the identity matrix, which is analogous to multiplying a number by its reciprocal.
In simple terms: A×A−1=A−1×A=I
Where:
- AA is the original matrix.
- A−1A^{-1} is the inverse of the matrix.
- II is the identity matrix, which is the equivalent of “1” in matrix operations.
The identity matrix is a square matrix with ones on the diagonal and zeros elsewhere. For example, the identity matrix for a 2×2 matrix looks like this:
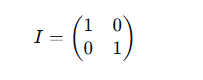
Understanding how matrix inversion works is vital, as it allows you to reverse transformations or solve systems of linear equations efficiently. It’s widely used in computational fields and practical applications.
When Do You Need Matrix Inversion?
Matrix inversion is required when you need to solve systems of linear equations or perform linear transformations in many fields. Here are just a few areas where matrix inversion is used:
1. Engineering: Solving Complex Systems
In engineering, matrices are often used to represent systems of forces, voltages, and even network flows. For example, in structural engineering, when analyzing a network of beams and forces, engineers use matrices to represent the forces acting on different parts of a structure. By inverting the matrix representing the system, they can solve for the unknown forces acting at specific points.
Example:
Imagine an engineering problem where multiple forces are applied to a bridge structure. These forces can be expressed as a system of linear equations. Matrix inversion provides a quick way to calculate the forces at various points without manually solving each equation.
2. Data Science and Machine Learning
In data science, particularly in linear regression, matrix inversion helps calculate the coefficients of the regression model. In linear regression, the goal is to find the line that best fits the data. The coefficients that define this line can be obtained using matrix operations, specifically by inverting matrices.
Example:
In a business scenario, you might want to predict sales based on advertising spend and other factors. By setting up a matrix equation and using matrix inversion, you can quickly calculate the optimal coefficients for the regression model, helping you make accurate predictions.
3. Cryptography
Matrix inversion is widely used in cryptography for encoding and decoding messages. In certain encryption algorithms, matrices are used to encrypt data. To decrypt the message, you need the inverse of the encryption matrix. Matrix inversion allows for secure, reversible transformations of data.
Example:
In a simple encryption algorithm, a message is represented as a matrix, and a key matrix is used to transform the message into its encrypted form. To decrypt, you multiply the encrypted message by the inverse of the key matrix, recovering the original message.
How to Use an Inverse Matrix Calculator
While matrix inversion can seem complex at first glance, modern technology has made it much easier. With the help of an Inverse Matrix Calculator, you can calculate the inverse of matrices of any size with just a few clicks.
Let’s break down how to use an inverse matrix calculator:
Step 1: Identify the Matrix You Need to Invert
First, you need a square matrix (i.e., the number of rows and columns must be equal). For example, consider a simple 2×2 matrix:
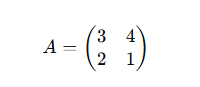
Step 2: Input the Matrix into the Calculator
Once you have the matrix, go to an Inverse Matrix Calculator tool online. You’ll find input fields where you can type in the numbers for each position in the matrix.
Visit Inverse Matrix Calculator to start using the tool and input your matrix values.
Step 3: Click Calculate
After inputting the matrix, click the Calculate button. The calculator will automatically compute the inverse matrix, provided the matrix has a non-zero determinant.
For the matrix AA, the result of the inverse calculation would be:
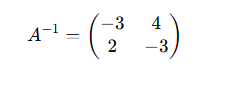
Step 4: Verify the Results
Finally, it’s important to verify the result. Multiply the original matrix by its inverse. If the result is the identity matrix, you’ve got the correct inverse! A×A−1=I
While using an Inverse Matrix Calculator is quick and efficient, there are some common mistakes you should be aware of:
- Non-Invertible Matrices: If the determinant of the matrix is zero, it does not have an inverse. Always check the determinant first.
- Incorrect Input: Be sure to input the matrix correctly. Even a small mistake in the values will lead to incorrect results.
- Skipping the Verification Step: After calculating the inverse, always verify it by multiplying the original matrix by its inverse to ensure it equals the identity matrix.
Conclusion:
Matrix inversion is a crucial tool for solving complex systems of equations, optimizing machine learning models, and securing data in cryptography. Whether you’re an engineer analyzing forces, a data scientist building predictive models, or someone working with encrypted data, mastering matrix inversion can make your work more efficient and accurate.
Using an Inverse Matrix Calculator makes this powerful tool accessible to everyone. No more manually calculating determinants or performing complex calculations—just input your matrix, click calculate, and get the inverse matrix instantly.
Start using an Inverse Matrix Calculator today to simplify your problem-solving process, and unlock the potential of matrix operations in your work!
For a deeper dive into matrix operations and applications, visit Khan Academy’s Linear Algebra Course for more in-depth explanations and interactive exercises.