When a matrix is not square or is singular, you can’t compute a regular inverse. That’s where the pseudo inverse (Moore–Penrose inverse) comes in. It extends the idea of an inverse to any matrix—rectangular, rank-deficient, or square but singular. In this guide, we’ll explain what the pseudo inverse is, how to calculate it, and when to use it.
What Is the Pseudo Inverse?
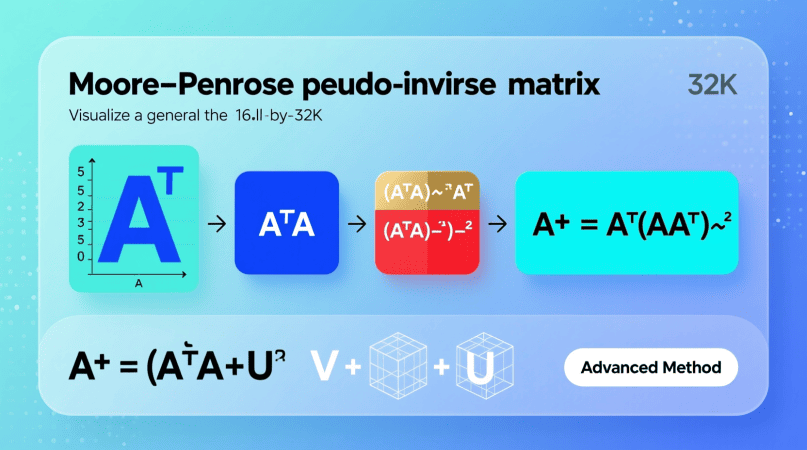
The pseudo inverse of a matrix AA, written as A+A^{+}, is a generalization of the inverse.
- If AA is square and invertible, then A+=A−1A^{+} = A^{-1}.
- If AA is rectangular or singular, A+A^{+} provides a “best fit” solution.
It’s widely used in linear regression, least squares problems, control theory, and signal processing.
Formula for Pseudo Inverse
There are three main cases:
- Full Column Rank (tall matrix, m≥nm \geq n) A+=(ATA)−1ATA^{+} = (A^T A)^{-1} A^T
- Full Row Rank (wide matrix, m≤nm \leq n) A+=AT(AAT)−1A^{+} = A^T (A A^T)^{-1}
- General Case (any matrix, any rank) – Use Singular Value Decomposition (SVD): A=UΣVT⇒A+=VΣ+UTA = U \Sigma V^T \quad \Rightarrow \quad A^{+} = V \Sigma^{+} U^T where Σ+\Sigma^{+} is formed by taking reciprocals of the nonzero singular values in Σ\Sigma and transposing.
Step-by-Step Example
Let’s compute the pseudo inverse of a 3×2 matrix: A=[123456]A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}
Since it has more rows than columns (tall matrix, full column rank), use: A+=(ATA)−1ATA^{+} = (A^T A)^{-1} A^T
Step 1: Compute ATAA^T A: ATA=[35444456]A^T A = \begin{bmatrix} 35 & 44 \\ 44 & 56 \end{bmatrix}
Step 2: Invert ATAA^T A: (ATA)−1=154[56−44−4435](A^T A)^{-1} = \frac{1}{54} \begin{bmatrix} 56 & -44 \\ -44 & 35 \end{bmatrix}
Step 3: Multiply by ATA^T: A+=(ATA)−1ATA^{+} = (A^T A)^{-1} A^T
This gives a 2×3 pseudo inverse matrix.
Using Singular Value Decomposition (SVD)
For the most general case:
- Decompose AA into UΣVTU \Sigma V^T.
- Replace each nonzero singular value σ\sigma in Σ\Sigma with 1/σ1/\sigma.
- Transpose the result → Σ+\Sigma^{+}.
- Compute A+=VΣ+UTA^{+} = V \Sigma^{+} U^T.
This method works for any matrix and is the standard in software packages.
Verification
The pseudo inverse satisfies the Moore–Penrose conditions:
- AA+A=AA A^{+} A = A
- A+AA+=A+A^{+} A A^{+} = A^{+}
- (AA+)T=AA+(A A^{+})^T = A A^{+}
- (A+A)T=A+A(A^{+} A)^T = A^{+} A
In practice, you can quickly check by multiplying AA+A A^{+} and A+AA^{+} A.
Applications
- Least Squares Solution: Solve Ax=bAx = b when AA is not square: x=A+bx = A^{+} b
- Machine Learning: Linear regression, dimensionality reduction.
- Engineering: Control systems, signal processing, optimization.
Computing with Software
Instead of doing everything by hand, you can use built-in functions:
- Python (NumPy):
import numpy as np A = np.array([[1,2],[3,4],[5,6]]) A_pinv = np.linalg.pinv(A) print(A_pinv) - MATLAB / Octave:
pinv(A) - R (MASS package):
library(MASS) ginv(A) - Excel / Google Sheets: Not directly available, but you can use custom scripts.
For quick verification, try the inverse matrix calculator, which can handle both regular inverses and pseudo inverses.
Common Mistakes to Avoid
- Forgetting that pseudo inverse ≠ regular inverse for non-square matrices.
- Using (ATA)−1AT(A^T A)^{-1} A^T when ATAA^T A is singular.
- Ignoring zero singular values in SVD (leads to divide-by-zero errors).
- Relying on manual calculation for large matrices—better to use software.
FAQs
Q: What is the difference between inverse and pseudo inverse?
A: Regular inverse exists only for square, non-singular matrices. The pseudo inverse exists for all matrices.
Q: Can I compute pseudo inverse for non-square matrices?
A: Yes, that’s one of its main purposes.
Q: Which method is best: formula or SVD?
A: Use SVD for stability and generality; formulas are fine for small, full-rank matrices.
Q: How do I verify my pseudo inverse?
A: Check AA+A=AA A^{+} A = A and A+AA+=A+A^{+} A A^{+} = A^{+}.
Q: Is pseudo inverse used in regression?
A: Yes, it provides the least squares solution when solving Ax=bAx = b.