Finding the inverse of a matrix is one of the most common tasks in linear algebra. Whether you’re solving systems of equations, working on graphics transformations, or coding in Python, knowing how to calculate the inverse of a matrix step by step makes the process much easier.
In this guide, we’ll go through definitions, simple formulas, row operation methods, examples, and even how to check if a matrix can’t be inverted. You’ll also see code snippets and a shortcut if you’d rather use a ready-made matrix inverse calculator.
What Does the Inverse of a Matrix Mean?
The inverse of a square matrix AA is another matrix A−1A^{-1} such that: A×A−1=IA \times A^{-1} = I
where II is the identity matrix (like the “1” in normal multiplication).
👉 A matrix must be square (same number of rows and columns) and have a non-zero determinant to be invertible. If the determinant is zero, the matrix is called singular and has no inverse.
Method 1: Formula for a 2×2 Matrix
For a simple 2×2 matrix: A=[abcd]A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
the inverse is: A−1=1ad−bc[d−b−ca]A^{-1} = \frac{1}{ad – bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
- Step 1: Compute the determinant ad−bcad – bc.
- Step 2: Swap aa and dd, change the signs of bb and cc.
- Step 3: Divide everything by the determinant.
Example: A=[4726]A = \begin{bmatrix} 4 & 7 \\ 2 & 6 \end{bmatrix}
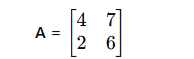
Determinant = 4(6)−7(2)=104(6) – 7(2) = 10. A−1=110[6−7−24]=[0.6−0.7−0.20.4]A^{-1} = \frac{1}{10} \begin{bmatrix} 6 & -7 \\ -2 & 4 \end{bmatrix} = \begin{bmatrix} 0.6 & -0.7 \\ -0.2 & 0.4 \end{bmatrix}
Method 2: Cofactor (Adjugate) Method for Larger Matrices
For a general n×nn \times n matrix: A−1=1∣A∣ adj(A)A^{-1} = \frac{1}{|A|} \, \text{adj}(A)
- Compute the determinant ∣A∣|A|.
- Find cofactors for each element.
- Transpose the cofactor matrix (this gives the adjugate).
- Divide by the determinant.
This method works for 3×3 or larger matrices, but it quickly becomes tedious by hand. A worked 3×3 example helps students, but for larger problems, it’s smarter to rely on computational tools.
Method 3: Gauss–Jordan Elimination (Row Operations)
The most systematic way to find a matrix inverse is by row reduction:
- Write the augmented matrix [A∣I][A | I].
- Use row operations to make the left side into the identity matrix.
- The right side will then be A−1A^{-1}.
Example (3×3): [211132100]→[100010001] ∣ A−1\begin{bmatrix} 2 & 1 & 1 \\ 1 & 3 & 2 \\ 1 & 0 & 0 \end{bmatrix} \quad \rightarrow \quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \; | \; A^{-1}
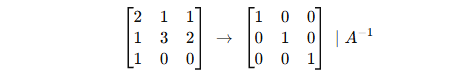
This approach is what most computer algorithms use, and it scales better than cofactors.
Method 4: Using Software or Calculators
In practice, especially for large matrices, you’ll rarely calculate inverses by hand. Instead, you can use software:
- Python (NumPy):
import numpy as np A = np.array([[2, 1], [5, 3]]) A_inv = np.linalg.inv(A) print(A_inv) - MATLAB / Octave:
inv(A) - R:
solve(A) - Excel / Google Sheets:
=MINVERSE(A1:B2)
Or, for quick results, just use an online inverse matrix calculator to instantly compute step-by-step solutions.
What if a Matrix Has No Inverse?
- If the determinant = 0, the matrix is singular.
- For non-square matrices, an inverse doesn’t exist.
- In applied math, you may use the pseudo-inverse (Moore–Penrose inverse) instead, especially in data science or regression problems.
Comparing the Methods
| Method | Best For | Pros | Cons |
|---|---|---|---|
| 2×2 Formula | Small matrices | Fast, simple | Only works for 2×2 |
| Cofactor / Adjugate | 3×3 or small | Theoretical clarity | Gets tedious quickly |
| Row Operations | Any size | Scalable, systematic | More steps by hand |
| Software / Calculator | Large matrices | Fast, accurate | Requires tools |
FAQs About Matrix Inverses
- How do I quickly check if a matrix is invertible? → Check if determinant ≠ 0.
- Can rectangular matrices have an inverse? → No, only square matrices.
- Is the inverse unique? → Yes, if it exists.
- What’s the difference between inverse and transpose? → Transpose flips rows/columns, inverse undoes multiplication.
- When should I use the pseudo-inverse? → For singular or non-square systems.