When learning linear algebra, one common question is: how can you calculate the inverse of a matrix using its determinant?
The determinant method is systematic and works for any square matrix, though it becomes more tedious as the size grows. In this guide, we’ll break down the adjugate method, show step-by-step examples, and explain how to check your result.
Why the Determinant Matters
A square matrix AA is invertible only if its determinant is not zero: det(A)≠0\det(A) \neq 0
- If det(A)=0\det(A) = 0, the matrix is singular and has no inverse.
- If det(A)≠0\det(A) \neq 0, then the inverse exists and can be found using:
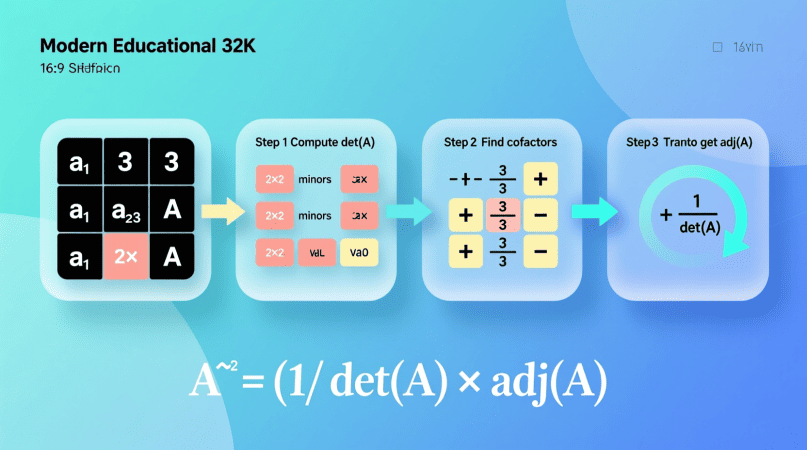
A−1=1det(A)⋅adj(A)A^{-1} = \frac{1}{\det(A)} \cdot \text{adj}(A)
where adj(A) is the adjugate (transpose of the cofactor matrix).
Step-by-Step Process
Step 1: Compute the Determinant
Start by calculating the determinant of the matrix.
- For 2×2: det(A)=ad−bc\det(A) = ad – bc.
- For 3×3 or larger: expand by minors (Laplace expansion) or use row reduction.
Step 2: Find Minors
For each entry, cross out its row and column → calculate the determinant of the smaller submatrix.
Step 3: Apply Cofactor Signs
Multiply each minor by (−1)i+j(-1)^{i+j} using the checkerboard pattern: [+−+−+−+−+]\begin{bmatrix} + & – & + \\ – & + & – \\ + & – & + \end{bmatrix}
Step 4: Build the Cofactor Matrix
Arrange all cofactors into a matrix.
Step 5: Take the Transpose
Transpose the cofactor matrix → this gives the adjugate matrix.
Step 6: Multiply by 1/det(A)1/\det(A)
Finally, divide each element of the adjugate by the determinant to get A−1A^{-1}.
Worked Examples
Example 1: 2×2 Matrix
A=[4726]A = \begin{bmatrix} 4 & 7 \\ 2 & 6 \end{bmatrix}
- det(A)=4(6)−7(2)=10\det(A) = 4(6) – 7(2) = 10.
- Swap diagonal → [6724]\begin{bmatrix} 6 & 7 \\ 2 & 4 \end{bmatrix}.
- Change signs of off-diagonal → [6−7−24]\begin{bmatrix} 6 & -7 \\ -2 & 4 \end{bmatrix}.
- Divide by 10 →
A−1=[0.6−0.7−0.20.4]A^{-1} = \begin{bmatrix} 0.6 & -0.7 \\ -0.2 & 0.4 \end{bmatrix}
Example 2: 3×3 Matrix
A=[123014560]A = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 5 & 6 & 0 \end{bmatrix}
- Determinant: −24+40−15=1-24 + 40 – 15 = 1.
- Compute minors and cofactors for all 9 elements.
- Cofactor matrix →
[−2420−518−1545−41]\begin{bmatrix} -24 & 20 & -5 \\ 18 & -15 & 4 \\ 5 & -4 & 1 \end{bmatrix}. - Transpose (adjugate) →
[−2418520−15−4−541]\begin{bmatrix} -24 & 18 & 5 \\ 20 & -15 & -4 \\ -5 & 4 & 1 \end{bmatrix}. - Divide by determinant (1).
So: A−1=[−2418520−15−4−541]A^{-1} = \begin{bmatrix} -24 & 18 & 5 \\ 20 & -15 & -4 \\ -5 & 4 & 1 \end{bmatrix}
Verification Step
Always verify by multiplying: A×A−1=IA \times A^{-1} = I
If the product equals the identity matrix, your inverse is correct.
Using Software and Tools
Manual calculation is useful for understanding, but large matrices are tedious.
- Python / NumPy:
import numpy as np A = np.array([[1,2,3],[0,1,4],[5,6,0]]) print(np.linalg.inv(A)) - MATLAB / Octave:
inv(A) - Excel / Google Sheets:
=MINVERSE(A1:C3) - Online tool: For quick results, try this inverse matrix calculator to verify your steps.
Common Mistakes
- Forgetting to check determinant ≠ 0.
- Mixing up sign pattern in cofactors.
- Skipping the transpose when forming adjugate.
- Arithmetic slips with fractions or decimals.
- Rounding errors when determinant is very small.
Comparing Methods
| Method | Best For | Pros | Cons |
|---|---|---|---|
| Determinant / Adjugate | Theory, small matrices | Shows concept clearly | Tedious for big matrices |
| Row Operations (Gauss–Jordan) | Larger matrices | Systematic, less formula | Many steps |
| Software / Calculator | Real use, verification | Fast, accurate | Requires tool |
FAQs
Q: What is the formula for inverse using determinant?
A: A−1=1det(A) adj(A)A^{-1} = \frac{1}{\det(A)} \, \text{adj}(A).
Q: When does determinant method fail?
A: If det(A)=0\det(A) = 0, the matrix has no inverse.
Q: Can I use fractions or decimals in this method?
A: Yes, but be careful with arithmetic.
Q: Why transpose the cofactor matrix?
A: Because the adjugate is defined as the transpose of the cofactor matrix.
Q: How to quickly verify?
A: Multiply the original and inverse → result should be identity matrix.
Final Thoughts
Now you know how to calculate inverse matrix using determinant: compute the determinant, form cofactors, transpose to get adjugate, and divide by determinant. The method builds strong understanding, but for larger matrices, a reliable matrix calculator or software tool will save you time and errors.