The determinant of a matrix is one of the most important numbers in linear algebra.
It tells you whether a matrix can be inverted, how transformations scale space, and whether systems of equations have a unique solution.
Let’s explore what the determinant really represents, how to calculate it, and why it matters in mathematics and real-world applications.
What Is the Determinant of a Matrix?
The determinant is a scalar value (a single number) calculated from the elements of a square matrix.
It provides critical information about a matrix, including:
- Whether the matrix has an inverse
- The scaling factor of a transformation
- The area or volume distortion caused by that transformation
- Whether a system of linear equations has one, infinite, or no solutions
If the determinant is zero, the matrix is singular — it has no inverse.
If the determinant is non-zero, the matrix is non-singular, meaning it can be inverted.
👉 You can instantly check this using our Determinant Calculator.
Determinant of a 2×2 Matrix
For a 2×2 matrix
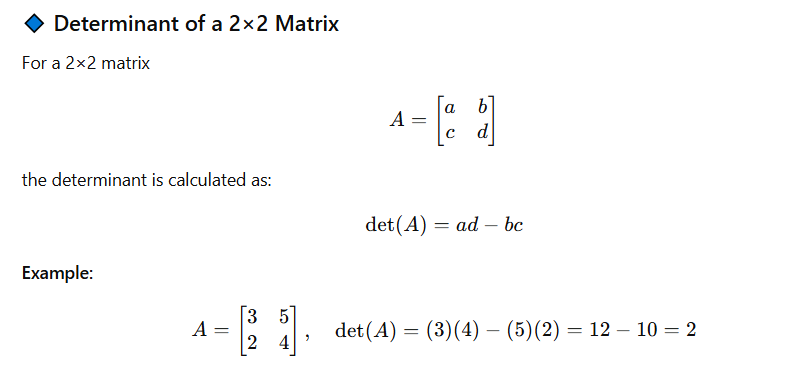
Since the determinant is not zero, this matrix is invertible.
You can verify this using the 2×2 Matrix Inverse Calculator.
Determinant of a 3×3 Matrix
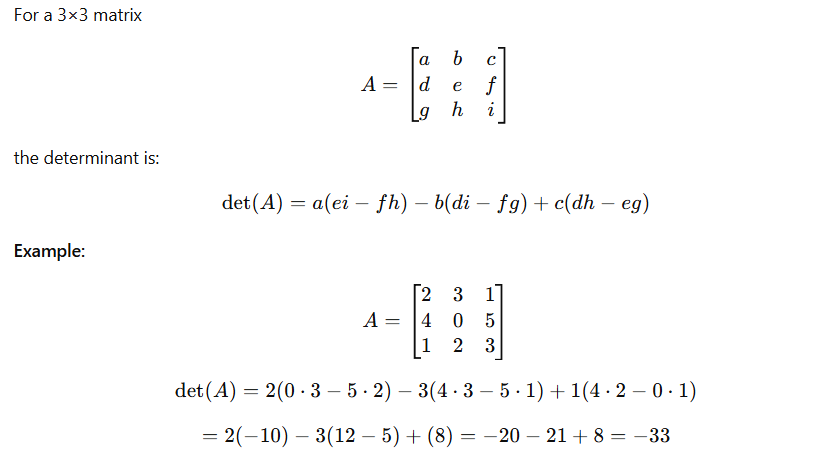
Since the determinant is nonzero ((-33)), this matrix is non-singular and has an inverse.
You can test it with our 3×3 Matrix Inverse Calculator.
Determinant of a 4×4 or Larger Matrix
For higher-order matrices, determinants are computed using cofactor expansion or row-reduction (Gauss–Jordan method).
Cofactor expansion along the first row:
[
\det(A) = \sum_{j=1}^{n} (-1)^{1+j} a_{1j} \det(M_{1j})
]
where (M_{1j}) is the minor matrix obtained by removing the first row and (j)-th column.
Although the formula expands rapidly, modern tools make this process fast — try our 4×4 Matrix Inverse Calculator or explore the Gauss–Jordan Method for manual computation.
Properties of Determinants
Understanding the properties of determinants simplifies large calculations and reveals matrix behavior.
| Property | Description |
|---|---|
| 1. det(AB) = det(A) × det(B) | Determinant of a product equals the product of determinants. |
| 2. det(Aᵀ) = det(A) | Determinant of a matrix equals that of its transpose. |
| 3. det(I) = 1 | The identity matrix always has a determinant of 1. |
| 4. det(kA) = kⁿ × det(A) | Multiplying a matrix by scalar k scales determinant by kⁿ, where n = order of matrix. |
| 5. det(A⁻¹) = 1 / det(A) | The determinant of the inverse is the reciprocal of the original. |
| 6. Swapping two rows or columns changes the sign of the determinant. | Shows the determinant’s sensitivity to order. |
| 7. If two rows (or columns) are identical, det(A) = 0. | Indicates linear dependence. |
| 8. If any row or column is all zeros, det(A) = 0. | No invertibility. |
These properties are vital when using elimination methods or simplifying complex systems of equations.
Geometric Interpretation
The determinant represents the scaling factor of the linear transformation described by a matrix.
- For 2D matrices, it gives the area scaling of a shape.
- For 3D matrices, it represents volume scaling.
- A negative determinant means the transformation flips orientation (reflection).
Example:
A 2×2 matrix with determinant = 3 triples the area of any 2D shape it transforms.
Determinant and Invertibility
A matrix is invertible (non-singular) iff its determinant ≠ 0.
[
A^{-1} = \frac{1}{\det(A)} \times \text{adj}(A)
]
If (\det(A) = 0), the inverse doesn’t exist.
You can confirm this instantly using our Inverse Matrix Calculator.
Determinant in Systems of Linear Equations
In linear algebra, determinants are used to determine if a system has a unique solution.
For the system (AX = B):
- If (\det(A) ≠ 0), the system has one unique solution.
- If (\det(A) = 0), the system has no or infinite solutions.
Cramer’s Rule expresses this relationship clearly:
[
x_i = \frac{\det(A_i)}{\det(A)}
]
where (A_i) is matrix (A) with the (i)-th column replaced by constants from (B).
You can practice solving these with our System of Equations Calculator.
Applications of Determinants
Determinants play a role far beyond textbook exercises. You’ll find them in:
- Machine Learning: Checking matrix invertibility in regression and covariance analysis.
- Computer Graphics: Determining rotation, scaling, and orientation in transformations.
- Engineering: Analyzing circuits, structural systems, and signal processing.
- Cryptography: Using modular determinants to encrypt messages.
- Statistics: Computing covariance matrices and multivariate distributions.
Understanding how determinants behave provides insight into why these fields rely on them.
common Mistakes When Finding Determinants
- Forgetting that only square matrices have determinants.
- Mixing up element positions during cofactor expansion.
- Ignoring sign alternation ((-1)^{i+j}) when computing minors.
- Assuming a zero determinant means “no solution” instead of “dependent equations.”
Check your work with an automated tool — it’s faster and helps you visualize where errors occur.
Summary Table
| Concept | Meaning |
|---|---|
| Definition | Scalar value showing invertibility & transformation scaling |
| det(A) = 0 | Matrix is singular (no inverse) |
| det(A) ≠ 0 | Matrix is non-singular (invertible) |
| Applications | Inverse matrices, geometry, data science, ML |
| Key Formula (2×2) | ad − bc |
| Key Formula (3×3) | a(ei − fh) − b(di − fg) + c(dh − eg) |
Frequently Asked Questions
What is the determinant in simple words?
It’s a number that shows how a matrix scales or transforms space — and whether it’s invertible.
Does every matrix have a determinant?
No. Only square matrices (same rows and columns) have determinants.
What does a determinant of zero mean?
The matrix cannot be inverted and represents a transformation that collapses space (for example, turning a square into a line).
Can I use determinants to solve equations?
Yes — through Cramer’s Rule and inverse matrices when (\det(A) ≠ 0).
