Complex Matrix Inverse Calculator
Instantly Calculate Matrix Inverses Online Fast, Accurate, and Easy to Understand
If you’re struggling with complex matrix algebra or want to save time in your math homework, data science project, or engineering assignment, you’re in the right place.
Our Matrix Inverse Calculator is designed to make finding the inverse of a matrix simple, fast, and accurate. Whether you’re a student, teacher, data analyst, or engineer, this free tool will help you calculate inverses of 2×2, 3×3, and even larger matrices in just seconds—no manual row operations required.
In this guide, you’ll learn:
- What a matrix inverse is and why it’s important
- How to use the Matrix Inverse Calculator effectively
- The benefits of using an AI-powered math tool
- Real-world examples where inverse matrices are crucial
- And answers to common questions from students and professionals
Let’s dive in and transform the way you work with matrices—once and for all.
What Is a Matrix Inverse?
Before using the tool, it’s helpful to understand what a matrix inverse actually is.
In linear algebra, the inverse of a matrix is another matrix that, when multiplied with the original, yields the identity matrix:
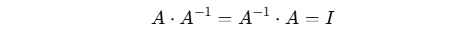
Here:
- A is your original matrix
- A⁻¹ is the inverse of matrix A
- I is the identity matrix (a square matrix with 1s on the diagonal and 0s elsewhere)
Not all matrices have inverses. A matrix must be:
- Square (same number of rows and columns)
- Non-singular (its determinant ≠ 0)
If these two conditions are met, the inverse exists and is unique.
How the Matrix Inverse Calculator Works
Our online tool takes your matrix as input and uses advanced linear algebra algorithms (like Gauss-Jordan elimination or LU decomposition) to:
- Check if the matrix is invertible
- Calculate the inverse accurately
- Present results in a clean, step-by-step format
Input Format
You simply enter your matrix values in a structured input field. For example:

You can enter:
- Integers
- Decimals
- Fractions (like
1/2) - Square matrices up to 10×10
Output Format
The result will show:
- The inverse matrix
- Steps used in the calculation (if enabled)
- Warnings if the matrix is not invertible
- Determinant value (to help you understand invertibility)
Why Use an Online Matrix Inverse Calculator?
Calculating an inverse manually can take 10–20 minutes, especially for larger matrices. Doing it wrong can lead to major calculation errors downstream—whether you’re solving systems of equations, programming algorithms, or modeling data.
Here’s why this tool is a game-changer:
| Benefit | Description |
|---|---|
| Accuracy | Eliminates human error in complex arithmetic. |
| Speed | Calculates large matrices (up to 10×10) instantly. |
| Learning Tool | Helps students understand the process via step-by-step breakdowns. |
| Professional Use | Useful for data science, engineering, simulations, and economics. |
| Saves Time | No need to manually compute determinants or cofactors. |
| Mobile-Friendly | Works on all browsers and mobile devices. |
How to Use the Matrix Inverse Calculator (Step-by-Step)
Using the calculator is incredibly simple. Follow this 5-step guide:
Step 1: Open the Tool
Go to the Matrix Inverse Calculator on your desktop or mobile browser.
Step 2: Enter Your Matrix
Input your matrix into the text field. For example:
[ [2, 3], [1, 4] ]
Or in expanded format:
2 3
1 4
Step 3: Choose Options (Optional)
Select:
- Show steps (to view solution steps)
- Round decimals (if needed)
- Fraction vs. decimal output
Step 4: Click “Calculate”
Press the “Calculate Inverse” button. The tool processes the matrix in real time.
Step 5: View and Use the Result
You’ll get:
- Inverse matrix (A⁻¹)
- Determinant
- Option to download or copy the result
How the Inverse is Calculated (Under the Hood)
We use standard matrix algebra algorithms:
- 2×2 Matrices:
For a 2×2 matrix
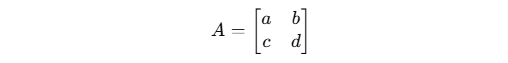
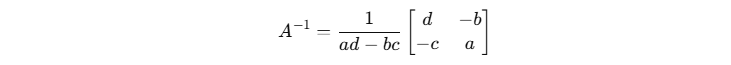
- 3×3 and Larger:
We use:
- Gauss-Jordan elimination
- LU decomposition
- Adjoint and cofactor matrix methods
Our system checks for singularity and computationally simplifies where possible.
Real-World Applications of Matrix Inverses
You might wonder: Why do matrix inverses matter?
Here are just a few areas where they’re critical:
Solving Linear Systems
In algebra, we solve AX = B using the inverse:

Data Science & Machine Learning
Inverse matrices appear in:
- Linear regression (Normal Equation)
- Optimization problems
- Dimensionality reduction
Cryptography
Inverse matrices help decode encrypted messages using matrix transformations.
Engineering Simulations
Used in systems of differential equations, structural analysis, and control systems.
Economics
Input-output models in economics use inverse matrices to predict sector changes.
Use Cases — Who This Calculator Is For
This tool is especially useful for:
| User Type | Use Case |
|---|---|
| Students | Algebra homework, understanding inverse steps |
| Teachers | Classroom demonstrations |
| Developers | Algorithm design & testing |
| Engineers | Circuit design, linear transformations |
| Data Scientists | Regression modeling, covariance matrices |
| Security Analysts | Cryptographic analysis |
Example: Solving a System Using the Inverse
Problem:
Solve the system:
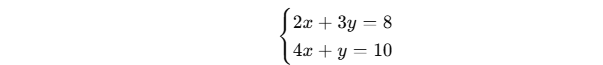
Step 1: Convert to Matrix Form
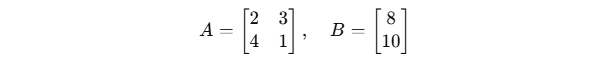
Step 2: Find A⁻¹ using the calculator
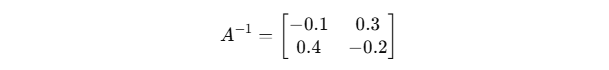
Step 3: Multiply
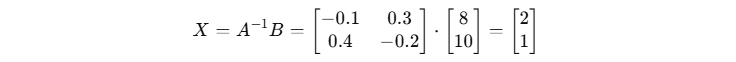
Final Answer: x = 2, y = 1
Frequently Asked Questions (FAQ)
1. What matrices can be inverted?
Only square, non-singular matrices can be inverted. The determinant must not be zero.
2. What happens if my matrix isn’t invertible?
The calculator will tell you it’s “non-invertible” and show the determinant as 0. You may need to check for redundancy in your equations or use other methods (like pseudoinverses or numerical solvers).
3. Can I input decimals or fractions?
Yes! Our tool accepts whole numbers, decimals (like 0.75), and fractions (3/4).
4. How large can the matrix be?
Currently, the tool supports up to 10×10 matrices. For larger sizes, consider numerical software like MATLAB or NumPy.
5. Does it show the steps?
Yes, if you select the “show steps” option. This is especially helpful for students or teachers.
6. Can I use it for homework or exams?
Absolutely! Just ensure you understand the steps (and don’t rely on it blindly).
7. Is the Matrix Inverse Calculator free?
Yes — 100% free to use online, anytime, on any device.
8. What if I want to multiply the inverse with another matrix?
After finding the inverse, you can use our Matrix Multiplication Calculator to continue solving.
Final Thoughts: Make Matrix Inversion Easy with the Right Tool
Manually calculating a matrix inverse is complex and error-prone. With our Matrix Inverse Calculator, you can bypass the grunt work, gain insights from step-by-step solutions, and save precious time—whether you’re studying, teaching, or applying math in the real world.
Start using the calculator today and see how simple linear algebra can be.
Use the Matrix Inverse Calculator Now
Would you like this formatted as an HTML article, blog post, or added to a CMS (like WordPress or Notion)? I can also help break it into sections with code examples or integrate it into your existing documentation.
