When you first learn about matrices, they might all look the same — a box of numbers.
But in linear algebra, there are many types of matrices, each with unique properties and uses.
This guide breaks them down with clear definitions, examples, and where you’ll actually see them in math, engineering, and data science.
Types of Matrices – Definitions, Examples, and Properties
1. Square Matrix
A square matrix has the same number of rows and columns.
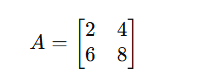
Here, (A) is a 2×2 square matrix.
Square matrices form the basis for most operations, such as determinants and inverses.
👉 You can compute the inverse of any square matrix with our Inverse Matrix Calculator.
2. Rectangular Matrix
A rectangular matrix has a different number of rows and columns.
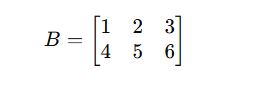
This is a 2×3 matrix — not square, so it has no determinant or inverse.
Rectangular matrices are often used in data tables and machine learning models, where rows represent samples and columns represent features.
3. Row Matrix and Column Matrix
- Row Matrix: Only one row
R = [1 5 9] - Column Matrix: Only one column
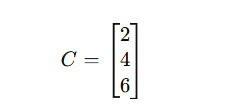
Row and column matrices are building blocks for operations like dot products and matrix multiplication.
If you’re exploring multiplication, check our Matrix Multiplication Guide for how these shapes interact.
4. Diagonal Matrix
A diagonal matrix has all off-diagonal elements equal to zero.

Only the main diagonal (top-left to bottom-right) has non-zero values.
Diagonal matrices simplify computation — multiplying or finding powers becomes much easier.
A special case is the identity matrix, discussed next.
5. Identity Matrix (Unit Matrix)
An identity matrix, denoted by (I), has 1s along the diagonal and 0s elsewhere.

Identity matrices are central in computing the inverse of a matrix using the Gauss–Jordan Method.
6. Zero or Null Matrix
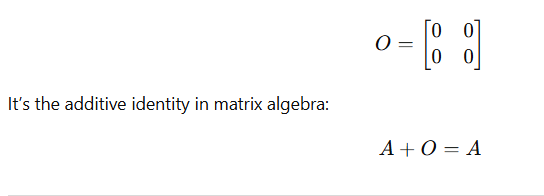
A zero matrix (or null matrix) has all elements equal to zero.
7. Triangular Matrices
Triangular matrices are used in numerical methods and solving systems of equations.
Upper Triangular
All elements below the diagonal are zero.
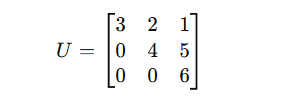
Lower Triangular
All elements above the diagonal are zero.
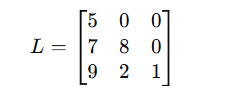
These are crucial in LU decomposition and matrix factorization, often implemented in software like MATLAB or Python NumPy.
8. Symmetric and Skew-Symmetric Matrices
Symmetric Matrix
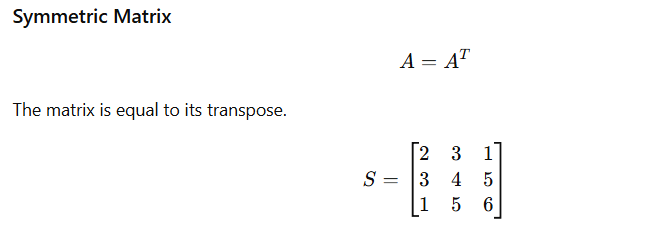
Symmetric matrices appear in covariance matrices in data science and physics.
Skew-Symmetric Matrix
A = -AT
All diagonal elements are 0.
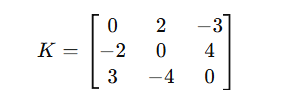
They are used in rotation transformations and advanced geometry.
9. Singular and Non-Singular Matrices
A singular matrix has a determinant of zero — meaning it can’t be inverted.
A non-singular matrix has a nonzero determinant and an inverse exists.
Check a matrix’s status with the Determinant Calculator.
10. Orthogonal Matrix
A matrix (A) is orthogonal if:
AT A = I
In simple terms, its rows and columns are perpendicular and normalized.
Orthogonal matrices are essential in 3D graphics and computer vision, where they represent pure rotations.
11. Sparse and Dense Matrices
- Sparse Matrix: Most elements are zero.
Used in data science and network analysis for large but mostly empty datasets. - Dense Matrix: Most elements are non-zero.
Common in small-scale algebra problems.
Efficient handling of sparse matrices saves memory and computing time in AI and simulation software.
12. Involutory Matrix
A matrix that is its own inverse:
A-1 = A
These are rare but useful for testing transformations where reversing twice returns the original state.
13. Idempotent Matrix
If (A^2 = A), the matrix is idempotent.
They appear in statistics (especially in projection matrices for regression).
14. Hermitian and Unitary Matrices
These appear mostly in complex-number mathematics and quantum computing.
- Hermitian: (A = A^*) (equal to its complex conjugate transpose).
- Unitary: (A^*A = I).
Both play a role in eigenvalue decomposition and advanced linear algebra.
Summary Table
| Type | Key Property | Common Use |
|---|---|---|
| Square | Rows = Columns | Determinant, Inverse |
| Diagonal | Nonzero diagonal only | Simplified computation |
| Identity | 1s on diagonal | Matrix inverse & Gauss–Jordan |
| Zero | All zeros | Additive identity |
| Symmetric | A = Aᵀ | Covariance, Physics |
| Orthogonal | AᵀA = I | 3D Graphics |
| Triangular | Half zeros | LU decomposition |
| Singular | det(A)=0 | Non-invertible check |
Why Knowing Matrix Types Matters
Understanding matrix types isn’t just theory — it’s the foundation for efficient problem-solving.
Each structure has shortcuts and special rules that save time and reduce complexity.
For instance:
- Using a diagonal matrix cuts computation cost.
- Knowing a matrix is symmetric helps in optimization.
- Recognizing a singular matrix prevents inversion errors.
Once you understand these patterns, advanced topics like eigenvalues, transformations, and data modeling become intuitive.
Explore Related Matrix Topics
- What Is a Matrix?
- How to Calculate the Inverse of a Matrix
- Matrix Inversion Explained
- Matrix Inverse in Machine Learning
Frequently Asked Questions
What are the main types of matrices in math?
Common types include square, diagonal, identity, symmetric, triangular, and zero matrices.
Which matrices are invertible?
Any square matrix with a non-zero determinant is invertible (non-singular).
What’s the simplest matrix type?
A row or column matrix — it’s the building block for all higher-dimensional matrices.
Where are different matrix types used?
From machine learning models to 3D rendering and encryption algorithms — matrices are everywhere.
