How to Find the Inverse of a Matrix Without Calculator – Step-by-Step Methods

Bysa2026sr

Sometimes you may be asked to find the inverse of a matrix by hand, especially in exams or when you’re learning the fundamentals of linear algebra. While calculators and software make this task faster, knowing the manual process helps you understand how inverses work and why some matrices don’t have one.

In this guide, we’ll cover:

  • Simple formula method for 2×2 matrices.
  • Adjoint (minors and cofactors) method for 3×3 matrices.
  • The Gauss–Jordan elimination method for larger matrices.
  • Tips for verifying your results without relying on a calculator.

If you want to cross-check your manual work later, you can always use the free Inverse Matrix Calculator to confirm your results.

Key Concepts to Remember

Before diving into the steps, here are some basics you must know:

  • Square Matrix: Only n×n matrices (like 2×2, 3×3) can be inverted.
  • Determinant Condition: If det(A) = 0, the matrix is singular and has no inverse.
  • Identity Matrix: When you multiply a matrix by its inverse, you should get the identity matrix (I).

Method 1: Formula for a 2×2 Matrix

For a matrix: A=[abcd]A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}

The inverse is: A−1=1ad−bc[d−b−ca]A^{-1} = \frac{1}{ad – bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}

Steps:

  1. Compute the determinant: det(A) = ad – bc.
  2. Swap the diagonal elements (a ↔ d).
  3. Change the signs of b and c.
  4. Multiply everything by 1det(A)\frac{1}{\text{det}(A)}.

✅ Example: A=[4321]A = \begin{bmatrix} 4 & 3 \\ 2 & 1 \end{bmatrix}

Det(A) = (4)(1) – (3)(2) = –2. A−1=1−2[1−3−24]=[−0.51.51−2]A^{-1} = \frac{1}{-2} \begin{bmatrix} 1 & -3 \\ -2 & 4 \end{bmatrix} = \begin{bmatrix} -0.5 & 1.5 \\ 1 & -2 \end{bmatrix}

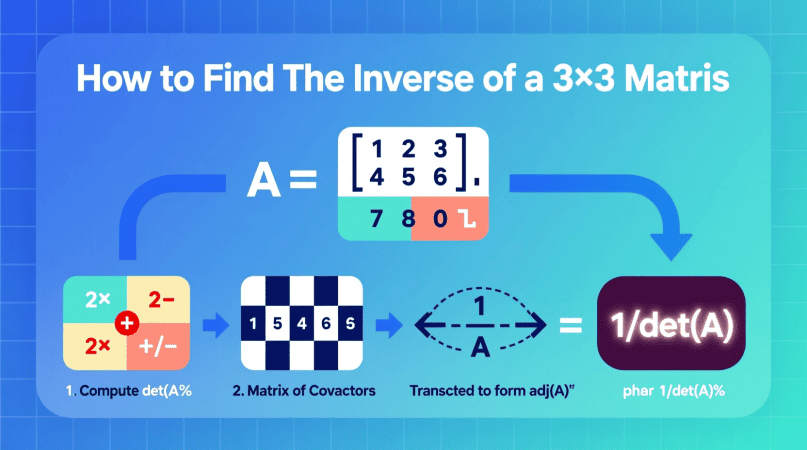
Method 2: Adjoint and Determinant Method for 3×3 Matrices

For a 3×3 matrix: A=[abcdefghi]A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}

Steps:

  1. Find the determinant:

det⁡(A)=a(ei−fh)−b(di−fg)+c(dh−eg)\det(A) = a(ei – fh) – b(di – fg) + c(dh – eg)

  1. Compute minors and cofactors for each element.
  2. Form the cofactor matrix.
  3. Transpose the cofactor matrix → this gives the adjugate matrix.
  4. Divide by determinant:

A−1=1det⁡(A)⋅adj(A)A^{-1} = \frac{1}{\det(A)} \cdot \text{adj}(A)

✅ Example:
If det(A) = 12 and the adjugate matrix is [6−2410−1−325]\begin{bmatrix} 6 & -2 & 4 \\ 1 & 0 & -1 \\ -3 & 2 & 5 \end{bmatrix}

Then: A−1=112[6−2410−1−325]A^{-1} = \frac{1}{12} \begin{bmatrix} 6 & -2 & 4 \\ 1 & 0 & -1 \\ -3 & 2 & 5 \end{bmatrix}

Method 3: Gauss–Jordan Elimination

This method works for any square matrix size and is often preferred for 3×3 or larger.

Steps:

  1. Write the augmented matrix [A | I], where I is the identity matrix.
  2. Use row operations (swap, multiply, subtract) until the left side becomes the identity.
  3. The right side will transform into A⁻¹.

✅ Example:
For a 3×3 matrix: [A∣I]=[211∣100132∣010100∣001][A | I] = \begin{bmatrix} 2 & 1 & 1 | 1 & 0 & 0 \\ 1 & 3 & 2 | 0 & 1 & 0 \\ 1 & 0 & 0 | 0 & 0 & 1 \end{bmatrix}

After performing row operations step by step, the right-hand side becomes the inverse.

Special Cases and Shortcuts

  • Diagonal Matrix: Inverse is just the reciprocal of each diagonal element.
  • Identity Matrix: Its inverse is itself.
  • Singular Matrix: If determinant = 0, no inverse exists.

How to Verify Your Manual Inverse

  • Multiply the original matrix by your result.
  • If the product = identity matrix, your inverse is correct.
  • If not, re-check the determinant, cofactors, or row operation steps.

For a quick cross-check, you can use an online tool like the Inverse Matrix Calculator to confirm your work.

Common Mistakes to Avoid

  • Forgetting to check if determinant ≠ 0 before starting.
  • Mixing up signs in cofactors.
  • Not transposing the cofactor matrix when using the adjoint method.
  • Arithmetic errors with fractions.

FAQs

Q1: Can all matrices be inverted manually?
No. Only square matrices with determinant ≠ 0 are invertible.

Q2: Which method is easiest without a calculator?
For 2×2 matrices, use the direct formula. For 3×3, the adjoint method works well. For larger, Gauss–Jordan is best.

Q3: How do I know if my inverse is correct?
Multiply A × A⁻¹. If the result = identity, your calculation is correct.

Q4: Is manual inversion practical for 4×4 or bigger?
It’s possible but tedious. Gauss–Jordan elimination is recommended.

Q5: Why does determinant = 0 mean no inverse?
Because the rows/columns are linearly dependent, making the matrix singular.

Similar Posts