How to Calculate Inverse of 3×3 Matrix – Formula, Steps, and Examples

If you’ve learned how to invert a 2×2 matrix, the natural next question is: how do you calculate the inverse of a 3×3 matrix? The process is a little longer but straightforward once you understand determinants, minors, and cofactors. In this guide, we’ll cover the formula method (adjugate approach), the row-operation method, and also show how to check your answer using software or a quick matrix calculator.

What Does the Inverse of a 3×3 Matrix Mean?

The inverse of a square matrix AA is another matrix A−1A^{-1} such that: A×A−1=IA \times A^{-1} = I

where II is the 3×3 identity matrix.

• If det⁡(A)≠0\det(A) \neq 0, the matrix is invertible.
• If det⁡(A)=0\det(A) = 0, the matrix is singular and has no inverse.

Formula for Inverse of a 3×3 Matrix

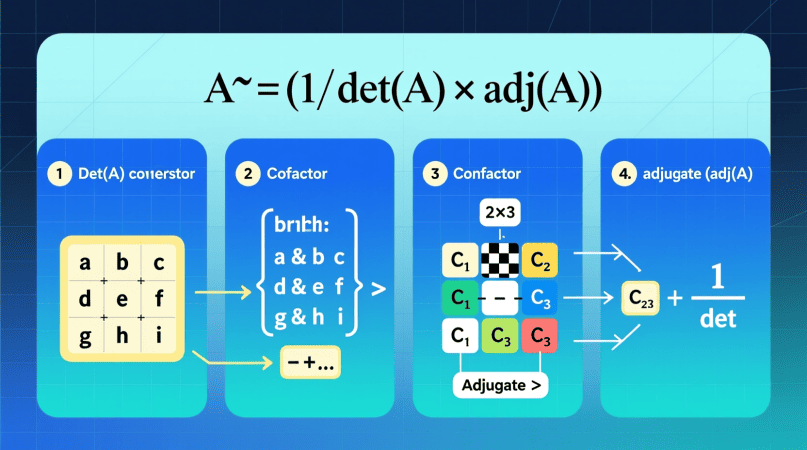
The general formula is: A−1=1det⁡(A)⋅adj(A)A^{-1} = \frac{1}{\det(A)} \cdot \text{adj}(A)

• det⁡(A)\det(A) = determinant of the matrix
• adj(A)\text{adj}(A) = transpose of the cofactor matrix

Step 1: Find the Determinant

For A=[abcdefghi]A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} det⁡(A)=a(ei−fh)−b(di−fg)+c(dh−eg)\det(A) = a(ei – fh) – b(di – fg) + c(dh – eg)

Step 2: Compute Minors and Cofactors

• The minor of each entry is the determinant of the 2×2 matrix left after removing its row and column.
• Apply the checkerboard sign pattern:

[+−+−+−+−+]\begin{bmatrix} + & – & + \\ – & + & – \\ + & – & + \end{bmatrix}

to get the cofactor matrix.

Step 3: Take the Transpose

Transpose the cofactor matrix → this gives the adjugate.

Step 4: Multiply by 1/det⁡(A)1/\det(A)

Divide every entry of the adjugate matrix by the determinant.

Worked Example

Let A=[123014560]A = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 5 & 6 & 0 \end{bmatrix}

Determinant: det⁡(A)=1(1⋅0−4⋅6)−2(0⋅0−4⋅5)+3(0⋅6−1⋅5)=−24+40−15=1\det(A) = 1(1\cdot 0 – 4\cdot 6) – 2(0\cdot 0 – 4\cdot 5) + 3(0\cdot 6 – 1\cdot 5) = -24 + 40 – 15 = 1

Since det⁡(A)=1\det(A) = 1, the matrix is invertible.

Cofactor matrix: [−2420−518−1545−41]\begin{bmatrix} -24 & 20 & -5 \\ 18 & -15 & 4 \\ 5 & -4 & 1 \end{bmatrix}

Adjugate (transpose): adj(A)=[−2418520−15−4−541]\text{adj}(A) = \begin{bmatrix} -24 & 18 & 5 \\ 20 & -15 & -4 \\ -5 & 4 & 1 \end{bmatrix}

Inverse: A−1=11×adj(A)=[−2418520−15−4−541]A^{-1} = \frac{1}{1} \times \text{adj}(A) = \begin{bmatrix} -24 & 18 & 5 \\ 20 & -15 & -4 \\ -5 & 4 & 1 \end{bmatrix}

Method 2: Row Operations (Gauss–Jordan)

Another way to invert a 3×3 matrix is by row operations:

1. Write the augmented matrix [A∣I][A | I].
2. Perform row operations to turn the left side into the identity matrix.
3. The right side becomes A−1A^{-1}.

This method is slower by hand but scales well and is what most algorithms use.

Using Software and Calculators

For larger or messy numbers, use tools to avoid arithmetic mistakes.

• Python (NumPy): import numpy as np A = np.array([[1,2,3],[0,1,4],[5,6,0]]) print(np.linalg.inv(A))
• MATLAB / Octave: inv(A)
• Excel / Google Sheets: =MINVERSE(A1:C3)
• Online tool: Try this inverse matrix calculator for instant results with step-by-step solutions.

Common Mistakes to Watch Out For

• Miscalculating the determinant.
• Forgetting to apply the sign pattern when computing cofactors.
• Not transposing the cofactor matrix.
• Dividing by zero when the determinant = 0.
• Arithmetic slips with fractions or decimals.

Quick Comparison of Methods

Method	Best For	Pros	Cons
Adjugate / Formula	Learning theory, clean numbers	Systematic, builds understanding	Tedious with messy entries
Row Operations	Larger matrices, teaching row reduction	Works for any size, consistent	Many steps, prone to error
Software / Calculator	Practical use, real-world problems	Fast, accurate	Requires tools

FAQs

Q: What is the formula for the inverse of a 3×3 matrix?
A: A−1=1det⁡(A) adj(A)A^{-1} = \frac{1}{\det(A)} \, \text{adj}(A).

Q: When does a 3×3 matrix have no inverse?
A: If the determinant is 0, the matrix is singular and cannot be inverted.

Q: How do I check my inverse is correct?
A: Multiply A×A−1A \times A^{-1}; it should return the identity matrix.

Q: Can I use decimals or fractions in the formula?
A: Yes, the formula works with any real numbers, but be careful with rounding.

Q: How do I invert a 3×3 matrix in Python?
A: Use numpy.linalg.inv() in NumPy.